如何用手指计算出恒星与地球的距离？

在公元前2 世纪，希腊天文学家依巴谷（Hipparchus）将恒星按照亮度分为6 个等级（称之为星等），最亮的恒星为一等星，肉眼可见的最暗的恒星为六等星。大约2 000 年后，在1856 年，英国天文学家波格森（N。 R.Pogson）对依巴谷星等的概念在数学上做了明确的定义。按照这个定义，星等差5 等相当于亮度差99 倍，即一等星的亮度为六等星的100 倍。

那些肉眼不可见的恒星则具有更高的星等。例如：比肉眼可见的极限亮度暗100 倍的恒星为十一等星（比六等星低5 个星等）。而那些比一等星更亮的恒星，它们则具有分数、零甚至负数星等。例如：织女星的视星等为0.03，天狼星的视星等则为-1.46，而金星（行星）亮度达到最大的时候它的视星等可达-4.4。

天文学家用视差原理来测量恒星的距离，下面的实验很好地展示这个原理。将手臂伸直，闭上左眼，用一根手指指向一个远处的物体，比如一棵树。此时保持手指不动，在睁开左眼的同时闭上右眼，你将会发现你的手指指向相对原来那个远处物体的方向发生了偏离。

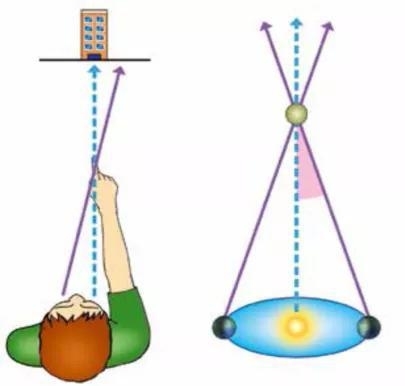
这种现象是由于你的两只眼睛并不完全在同一个位置造成的，它们之间有几厘米的距离。因此，当你用两只眼睛分别观察同一个前景物体（比如手指）的时候，两只眼睛的视线方向会稍微有一点差别。这种位置差别我们称之为视差。为了测量近邻恒星的距离，天文学家们首先在地球位于太阳一侧时（比如1 月份）先测量一次恒星的方位，当地球运动到相对太阳的另一侧时（7 月份）再次测量恒星的方位。由于两次测量时，地球位于相距较远的两点，因此测量的恒星方位将会有细微的差别。一年之中，恒星方位偏离其平均方位的最大值称为周年视差。一旦测得恒星的视差，由于地球绕太阳公转的轨道直径也是已知的（3 亿千米），因此只要用简单的三角法就可以计算出恒星的距离了。

由于恒星离我们十分遥远，所以恒星的视差其实是非常微小的。通常我们用度来表示角度，1 度分成60 角分，而1 角分又可以分为60 角秒。所以，1 角秒就等于1/60 个1/60（1/3 600）度。周年视差为一个角秒的恒星距离定义为一个秒差距，1 秒差距等于3.26 光年。恒星距离我们越远，周年视差就越小。例如：距离我们两秒差距的恒星，其周年视差为0.5角秒；而距离我们10 秒差距的恒星其周年视差就只有0.1 角秒了，以此类推。距离我们最近的恒星（半人马座比邻星）的视差为0.772角秒，相当于1.3 秒差距（4.2 光年）。

我们无法仅从某颗恒星的视亮度来判断它到底是一颗距离我们很近但实际亮度很低的恒星，还是一颗距离我们很远但实际亮度很高的恒星。不过，如果我们知道恒星发出的光有多少能够到达地球（通过测量视星等），同时又知道恒星与我们之间的距离（通过三角视差法测量），我们就能够测量恒星的绝对光度[6]。已知最亮恒星的光度比太阳高几十万倍，而最暗恒星的光度仅有太阳的几十万分之一。

来源： 我是科学家iScientist