随机过程多次跨阈概率的精确解析计算获新突破

科技日报记者 马爱平

记者获悉，机械、航空航天和土木工程领域跨学科学术期刊《力学系统与信号处理》（Mechanical Systems and Signal Processing）发表了长沙理工大学副教授张振浩课题组的研究论文《工程中Wiener过程与固定界限多次交叉的时间间隔》。

在结构动力可靠度分析领域，精确计算随机过程超越安全界限（可简称随机过程跨阈）的概率是一个关键科学问题，其主要难点是如何计算随机过程与界限交叉所派生出的随机变量的概率分布。

张振浩表示，已有的随机过程跨阈概率分析方法可基本可分为两类，一类是直接假定随机过程跨阈事件的性质（如著名的Possion假设），简化了分析过程，可以解析地求解随机过程跨阈概率；另一类是数值模拟法（如蒙特卡洛抽样等），可求得随机过程跨阈概率的数值近似解。第一类方法基于某种假定获得的解析解显然是非精确的，有时误差甚至大到不可接受；第二类方法计算效率低下，不便于工程应用。精确并解析地求解随机过程跨阈概率，一直是结构动力可靠度理论自1945年诞生以来的难题。

70多年来，关于这方面的研究取得了一些进展，获得了几个随机过程跨阈概率的精确解析解，但这些解均为关于首次跨阈问题的（如Wiener过程首次跨阈时间的概率密度函数精确解析解）。关于随机过程多次跨阈的精确解析解由于难度极大，一直未有突破。

张振浩等在上述论文中开拓性地研究了Wiener（维纳）过程多次跨阈概率的精确解析计算方法，在未采用任何数学假定的前提下推导出Wiener过程与固定界限任意两次相邻交叉的时间间隔的概率密度函数精确解析显式表达式。

专家表示，该成果是结构动力可靠度理论诞生70余年来首个关于随机过程多次跨阈问题的精确解析解，是随机过程领域里的一个原创性公式，具有极为重要的理论意义，并且在土木、海洋、机械、信号及金融等与Wiener过程有关的领域都有潜在的应用价值。

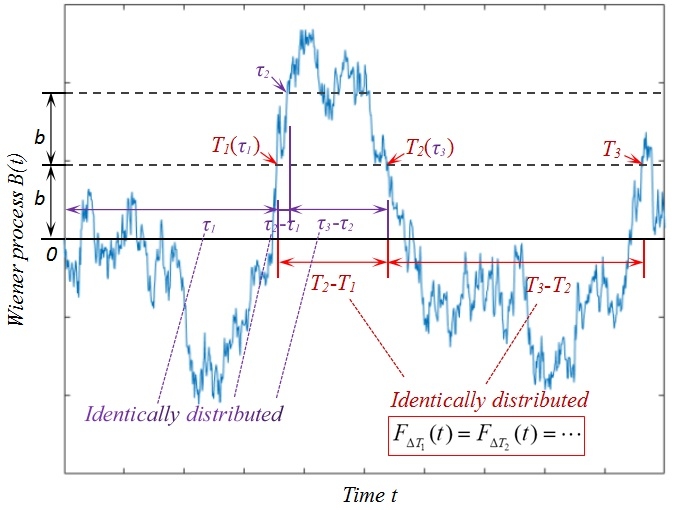
（论文论证了Wiener过程与固定界限任意相邻交叉的时间间隔具有相同概率分布）

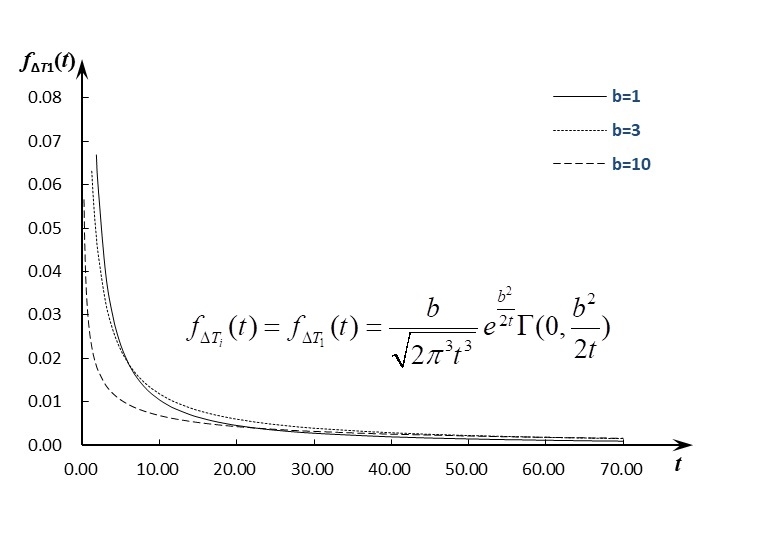
（Wiener过程与固定界限任意相邻交叉时间间隔的概率密度函数精确解析显式表达式及其函数图像）

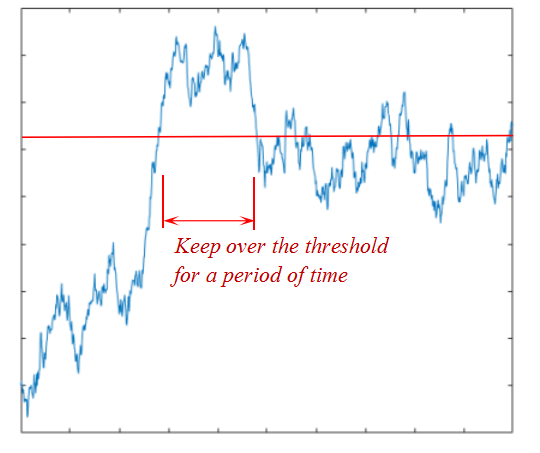
（基于时间间隔（持续时间）的首超破坏机制—结构响应超过阈值并持续一定时间导致结构失效）

此外，该论文还提出了一个重要的结构失效新准则：基于时间间隔（跨阈持续时间）的首超破坏准则。即，结构随机响应过程超过一定界限时并未立即失效，而是当结构响应超越阈值持续一定时间后结构才发生失效。该失效机制是对传统首超破坏机制的拓展。