理工男花40年时间,用圆规画1000张画,网友:太浪漫了!

来源:艺非凡
真正的艺术与美,
从来不是艺术馆里束之高阁的藏品,
而是自然界中的生灵与万物。
提起理工科男生,你想到什么?
理性、严谨、不苟言笑,
没有艺术细胞,还不懂浪漫。
其实,
这种印象或许根本上就是错的,
理工科男生的艺术和浪漫,
有可能是我们不懂。

比如委内瑞拉的理工科男生 Rafael Araujo,
表面上看起来是艺术绝缘体的他,
却用尺规画下了一系列令人震撼的作品。
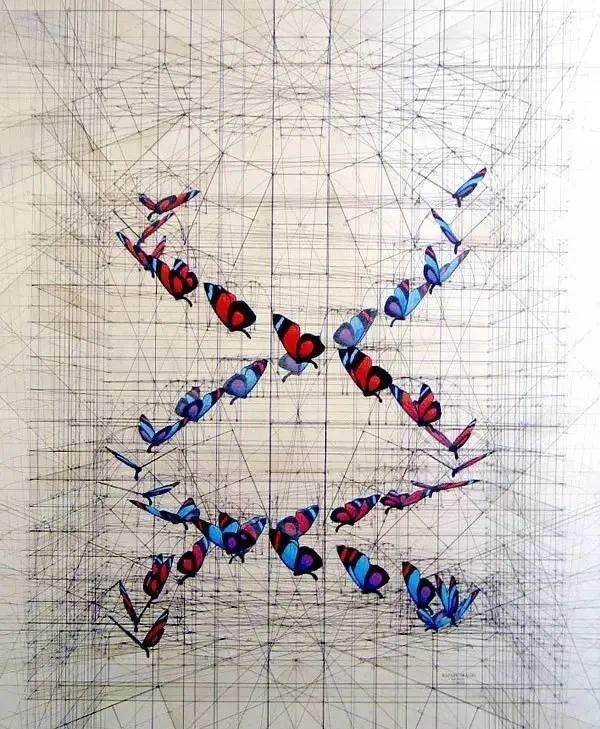
先放几张图片上来大家感受一下:

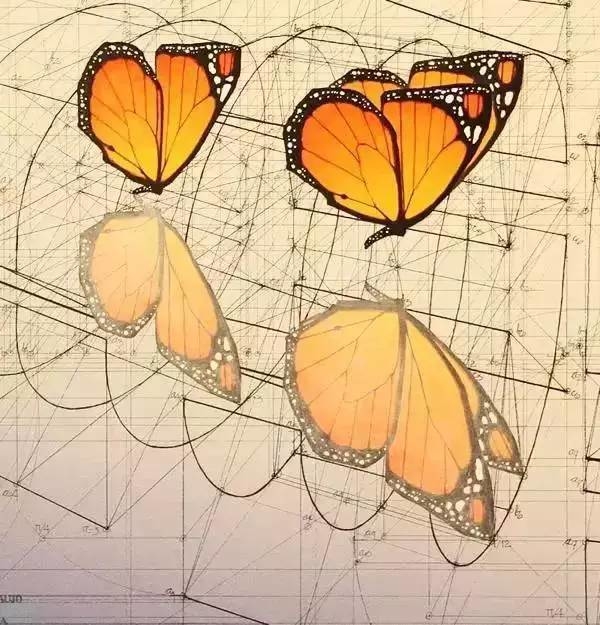

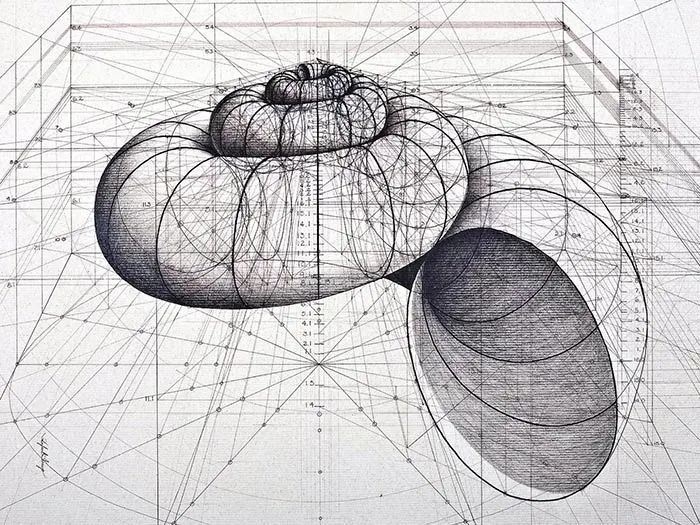
以上的三张全部都是
没有使用任何计算机绘图软件,
而是单靠铅笔、尺、量角器、
圆规等纯手绘出来的。
你能看出来吗?
对应的分别是海螺和蝴蝶的序列。
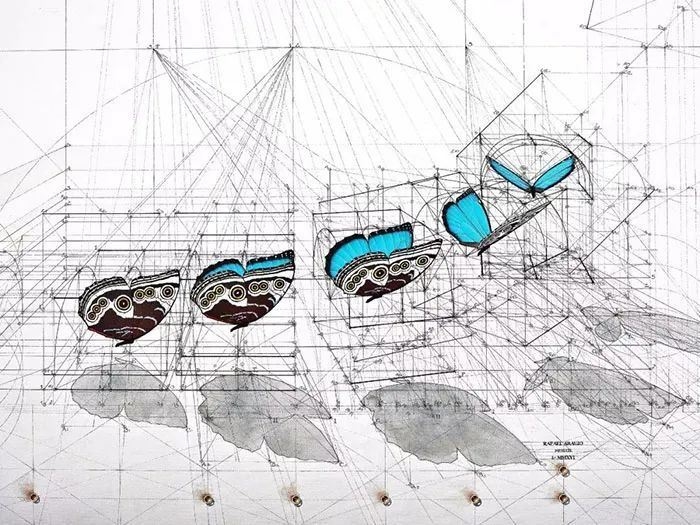
为什么说是序列?
因为 Rafael Araujo画的并不是,
海螺、蝴蝶,
而是数学序列,
不同的数学序列经过不同的组合,
最后诞生出了不同的图案。

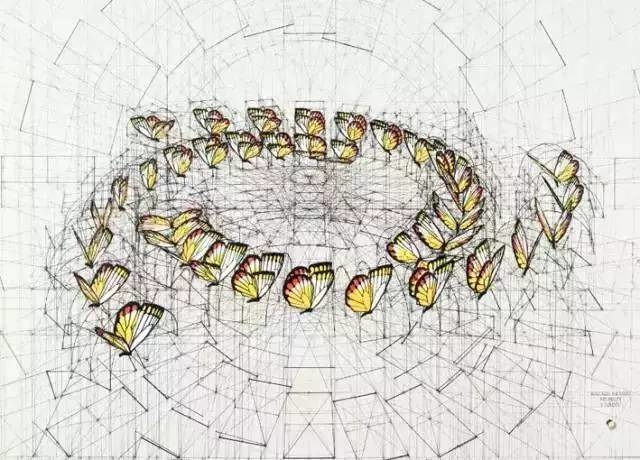
这些序列主要是由
著名的黄金分割、
黄金螺旋法则与斐波纳契数列,
与一些普通的对数曲线、
算术曲线和指数曲线
以及几何图案组成的。
Rafael Araujo管这种绘画模式叫做:
几何美学。

别看Rafael Araujo,
是一名理工男,
但是Rafael Araujo比任何一个人都懂艺术,
尤其是几何艺术。

在五六岁的时候,
他就发现山茶花有着世界上最完美的外形,
那时候他就开始思考:
是什么,
让山茶花这么美丽?
他尝试着把山茶花画下来,
然后用山茶花的外形中,去反推数学序列,
最终得到了它美丽的秘诀:
黄金比例。

Rafael Araujo恍然大悟:
原来,所有令我们感到美丽的东西,
比如盛开的山茶花、蝴蝶的翅膀、飞行的姿态和距离,
柳树上抽芽的叶子等等,
它们的美,都是因为黄金比例法则。
因此,Rafael Araujo认为,
黄金比例,是人类现有认知中美的极致。

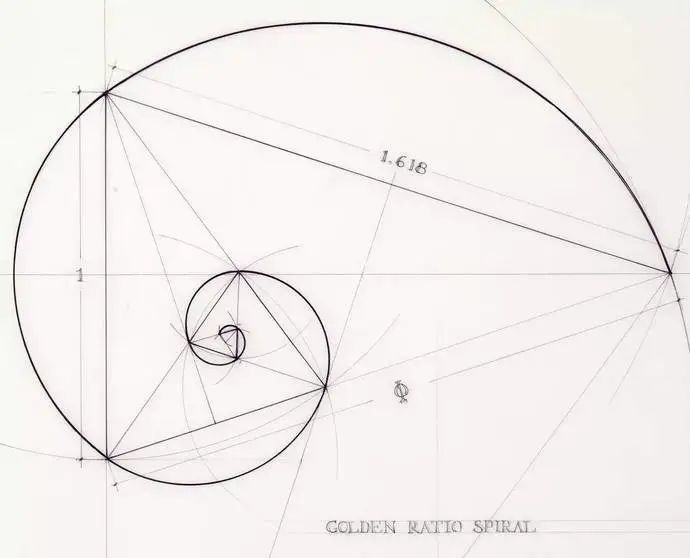
什么是黄金比例?
就是神秘奇幻的大自然序列,
费波那西数列,
(Successione di Fibonacci)。
指的是这样一个数列:
1、1、2、3、5、8、13、21、34……。
也可以写作:
F(1)=1,F(2)=1, F(n)=F(n - 1)+F(n - 2)
(n ≥ 3,n ∈ N*)
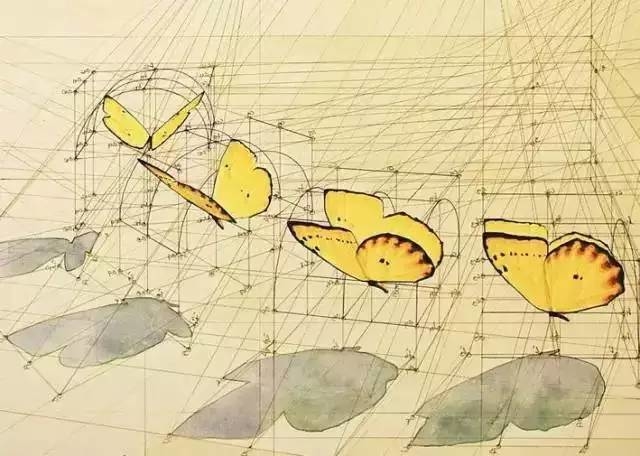
这个序列并不是人为创造的,
而是大自然创造后被人类发现的。
鲜花、飞鸟、动物、人体等等,
大自然中美的一切,
都和黄金比例有着极大的关系。
发现了这一奥秘之后,
Rafael Araujo的野心是:
在纸上复刻出大自然美的规律。
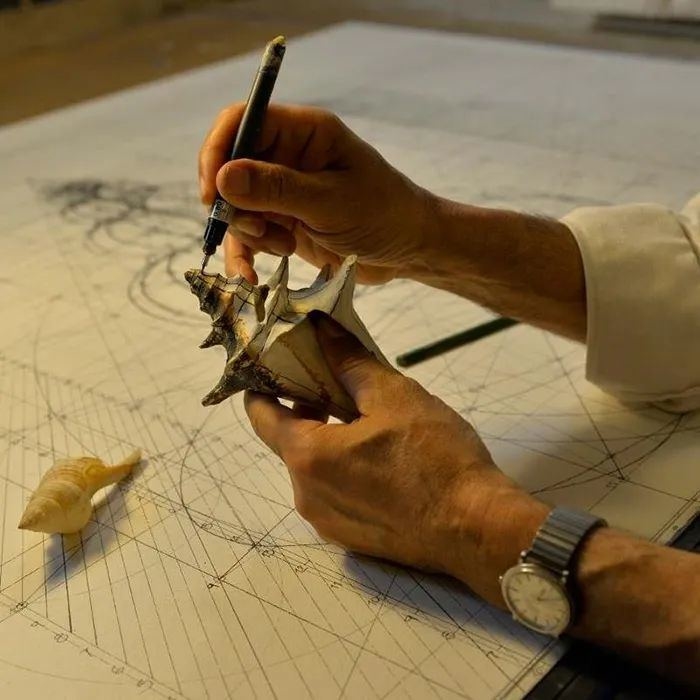
之后的40年,
他不断以圆规、尺规和铅笔等绘图工具,
尝试在纸上创造自然之美。
画出了一幅幅令人叹为观止的佳作。
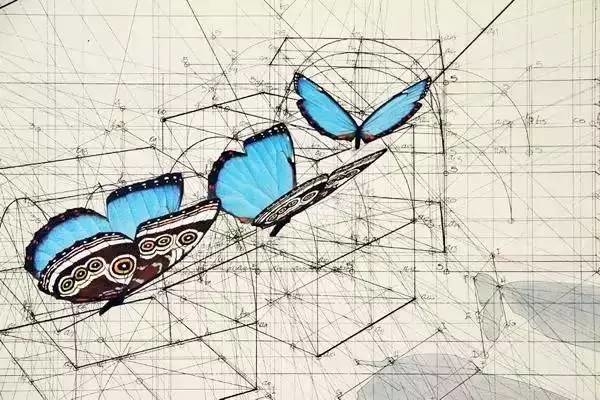
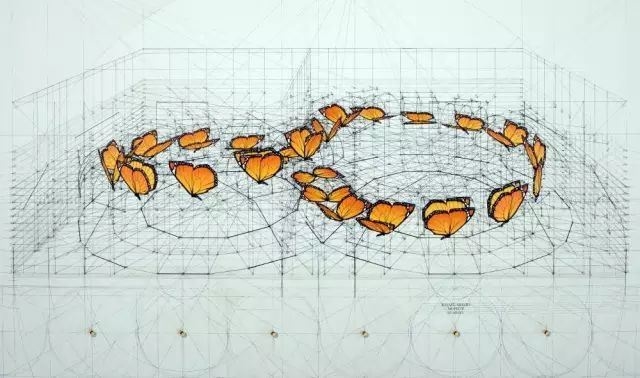
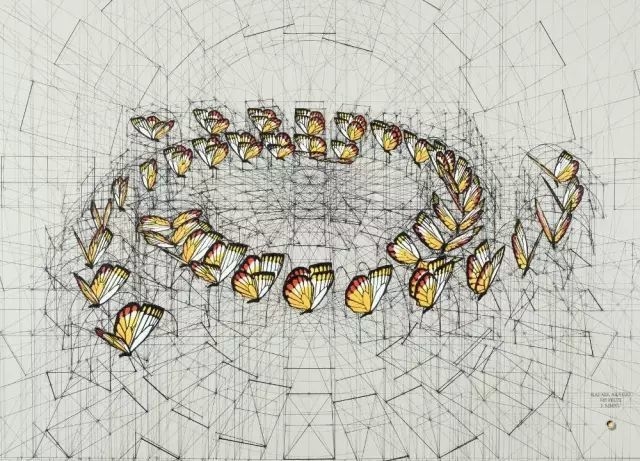
其中画的最多的就是蝴蝶以及蝴蝶的飞行轨迹,
因为“蝴蝶是自然之美的集大成者。”

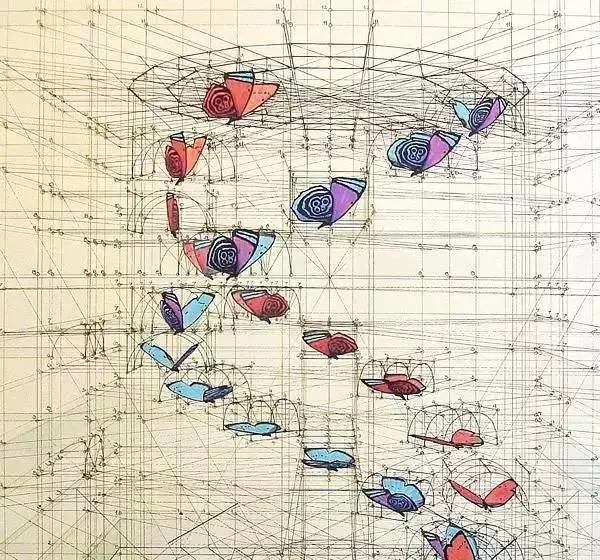
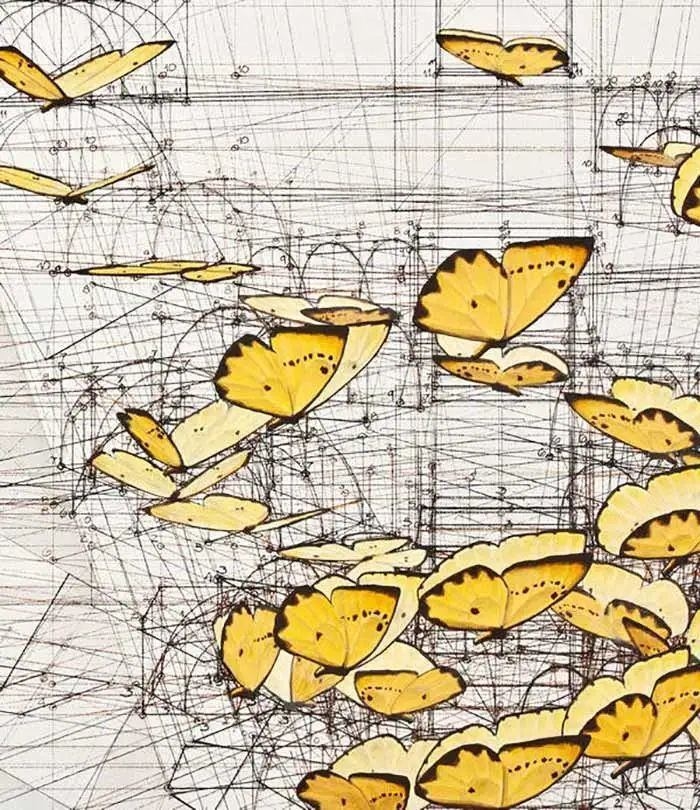
黄金比例,
有时候也叫作蝴蝶比例,
意思就是蝴蝶身长与双翅展开的长接近黄金分割比。
另外蝴蝶也符合蝴蝶曲线的理论,
这一切都让蝴蝶的外形看起来非常完美。
把Rafael Araujo的画放大五倍,
蝴蝶背后的数学奥秘就会一一显现。

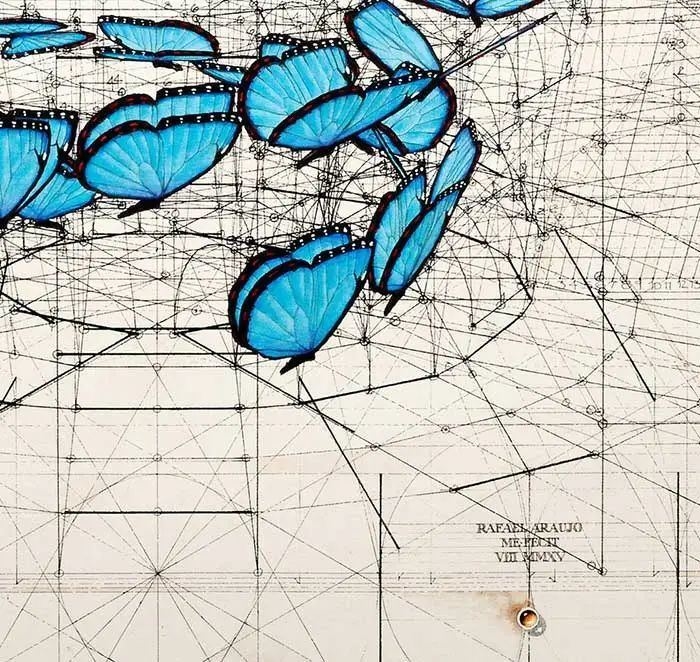

同样的还有海螺,
每当我们去海边捡贝壳、捡海螺的时候,
都会惊叹它们的外形是如此美丽。
但Rafael Araujo深知,
美丽的背后是无数数学理论的支撑。
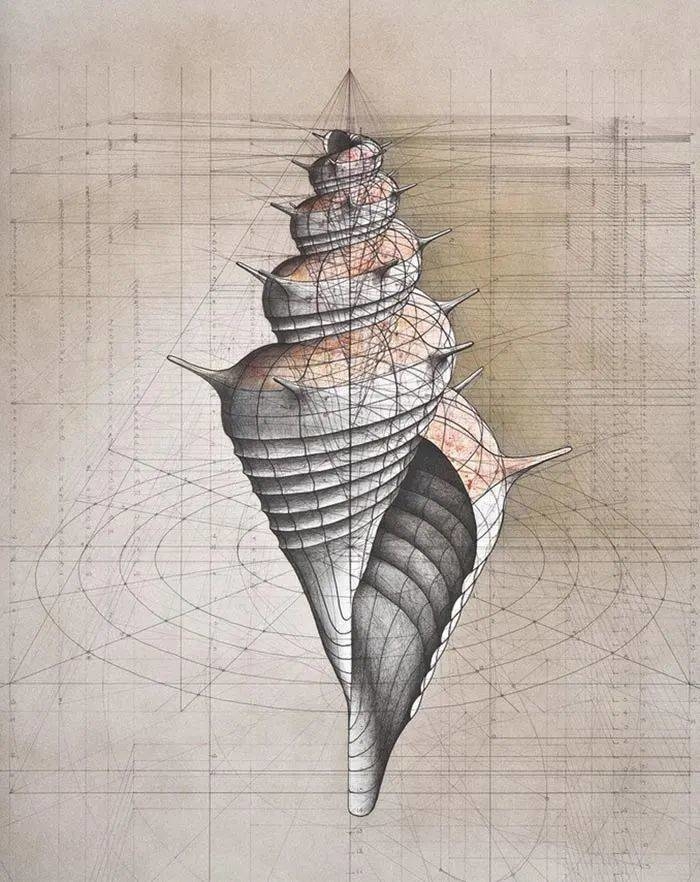
海螺生成需要遵循三个基本法则:
扩张、旋转和扭转。
所有的海螺,
都是先由一个很小很细的空心圆锥慢慢扩张、旋转、
扭转而形成的螺旋体,
该螺旋体一直是增量扩张,螺口最大。
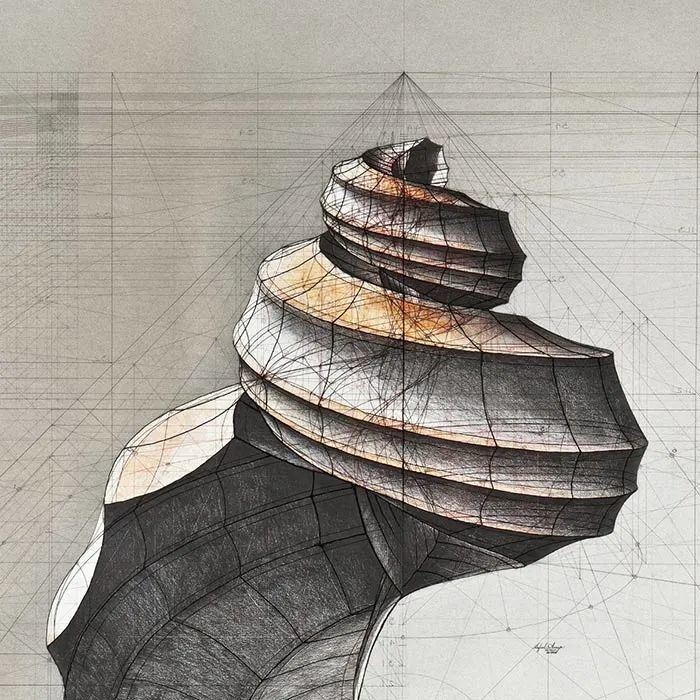
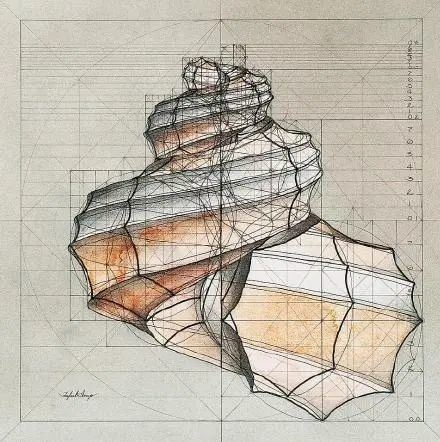
尽管螺形状各式各样、千奇百怪,
但都是全部遵循螺旋线,
包括但不限于:
等角螺线、阿基米德螺线、费马螺线、
等角螺线、双曲螺线、圆内螺线等等……
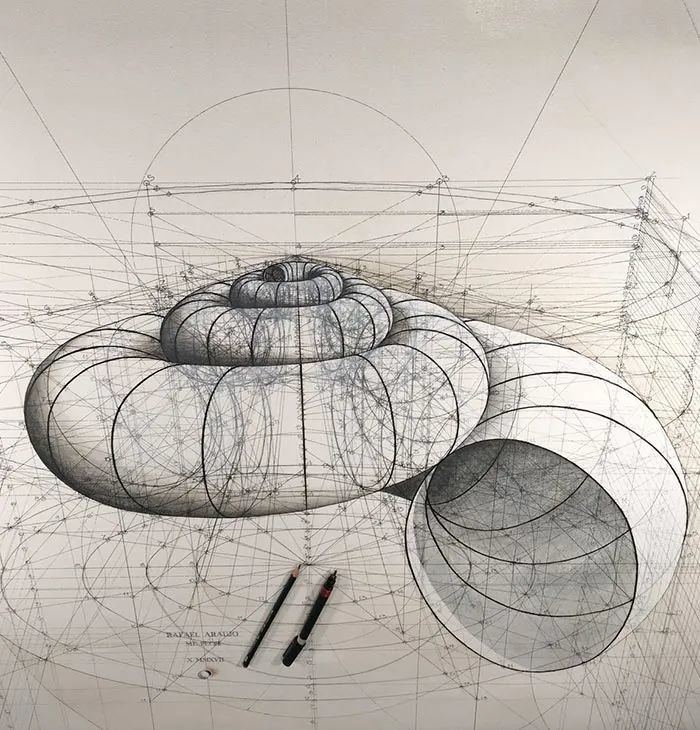
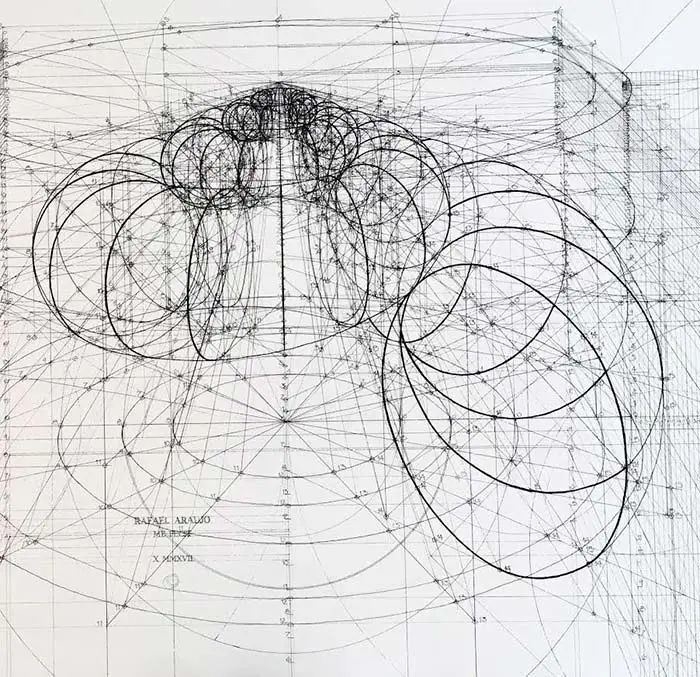

倘若你把这些螺旋线画出来,
你也能得到一个完美的海螺图形。

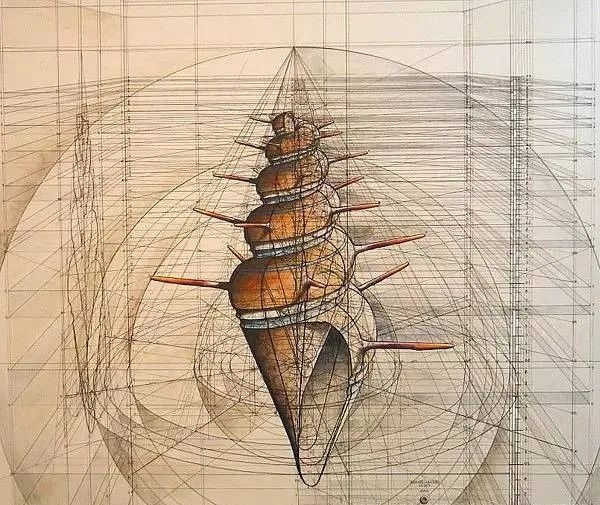
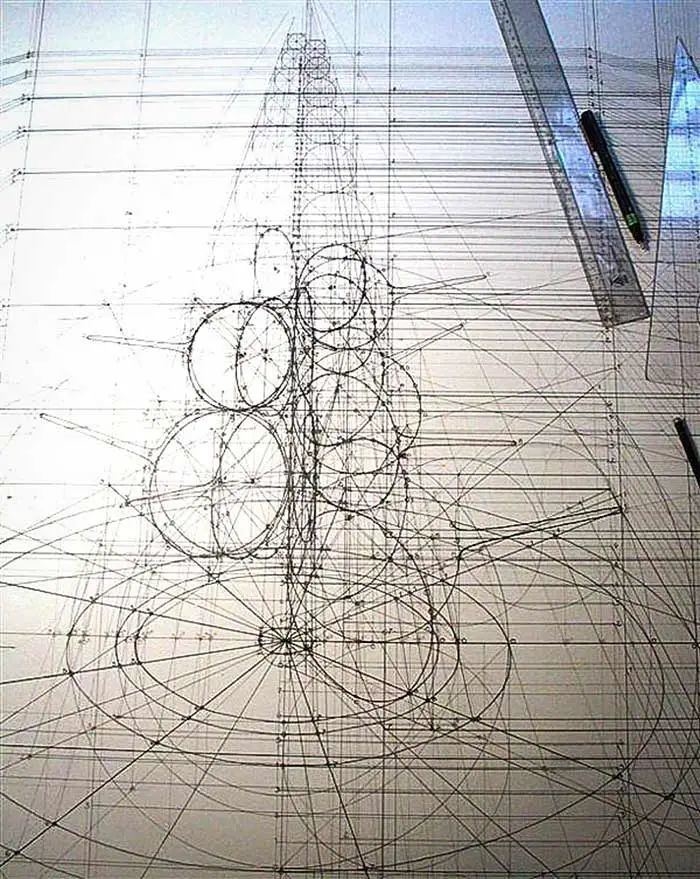
无论海螺、蝴蝶还是山茶花,
其实都是从一些基本图形上演变而来的。
这些基本图形,就是几何图形。

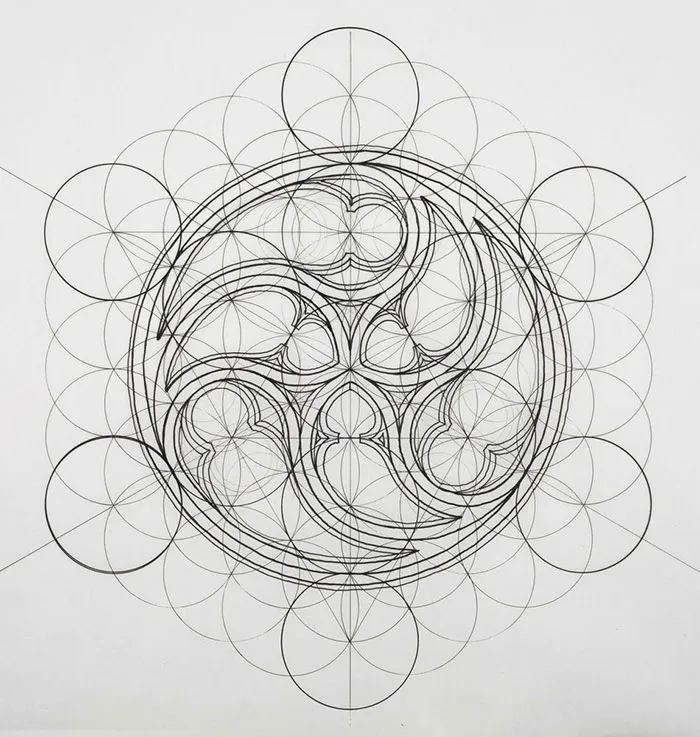
几何图形,
也符合黄金比例的规律。
我们常说的黄金三角形,
就符合1:1.618的黄金比例。
建立在黄金比例,
和其他数学理论基础上的蝴蝶,
也呈现出一种完美的飞翔姿态和轨迹,
多一寸则太多,少一寸则太少。

因为深谙数学之美,
对于建筑师Rafael Araujo而言,
这世界上没有蝴蝶和海螺,
没有叶子和绚烂的彩虹。
因为在他眼里,所有的一切都是数学规律。
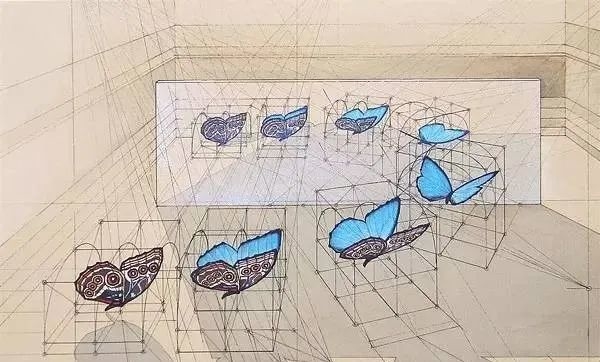

他就像是有一双透视眼一样,
在看待鲜花盛开的一刻,
他就知道这朵鲜花日后该有多少花瓣,
如何旋转,以及怎样盛放。
因为基本上所有的鲜花都遵循黄金比例法则:
像百合花,它有3个花瓣;
金凤花有5个花瓣;
菊苣有21个花瓣;雏菊有34个花瓣,……。
每个花瓣严格按照0.618034的黄金比例来放置,
才能保证花瓣最大限度地暴露在阳光下,
享受阳光与雨露。
这是达尔文适者生存法则的延续,
同时也是大自然鬼斧神工的杰作。